复合梁正应力分布规律实验
一、实验目的
1. 用电测法测定叠梁,复合梁在弯曲受力状态下,沿其横截面高度的正应变(正应力)分布规律。
2. 推导叠梁,复合梁的正应力计算公式。
二、实验仪器和设备
1. 纯弯曲梁实验装置(纯弯曲梁复合梁)。
2. 静态数字电阻应变仪。
三、实验原理及步骤
1. 实验原理
复合梁的材料为铝梁和钢梁,上层是铝梁,其弹性模量分别为E=70GN/m2和E=210GN/m2。复合梁上总过贴上了12各应变片,每个梁各6个。
1. 几何、物理和静力学关系
以材料尺寸相同的两层矩形截面复合梁在纯弯 曲情况下为计算模型,在其纵向对称面内,承受弯矩 M的作用。上梁的弹性模量为E1,横截面面积为A1,下梁的弹性模量为E2,横截面面积为A2,且A1=A2,单梁的梁宽和梁高分别为b和h,在其纵向对称面内,承受弯矩M的作用。两种不同的材料由胶粘合制成。下面建立横截面上的弯曲正应力公式,平面假设与单向假设均成立。
设中性层的曲率半径为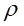 ,并沿截面纵向对称轴与中性轴分别建立坐标轴y与z,中性层离交界面的距离为e。
,并沿截面纵向对称轴与中性轴分别建立坐标轴y与z,中性层离交界面的距离为e。
(1)变形几何关系。根据平面假设可知,横截面上y处的纵向正应变为:
 (6-1)
(6-1)
(2)物理关系。依胡克定律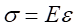 ,而
,而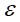 由式(1)带入,可以得出不同材料区的弯曲正应力分别为:
由式(1)带入,可以得出不同材料区的弯曲正应力分别为:
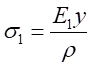 ,
,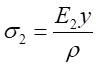 (6-2)
(6-2)
(3)静力学平衡关系。根据受力分析,由静力学平衡关系,考虑横截面上内力的平衡,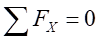 ,可以得出:
,可以得出:
 (6-3)
(6-3)
由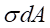 组成的内力系,在横截面上形成一个内力偶矩M,即为横截面上的弯矩M,即:
组成的内力系,在横截面上形成一个内力偶矩M,即为横截面上的弯矩M,即:
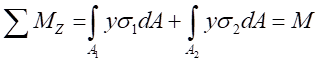 (6-4)
(6-4)
2. 确定中性层位置
将式(2)代入式(3)中,得
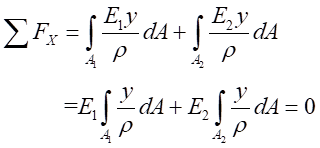
令
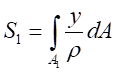
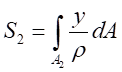
则
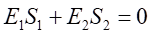 (6-5)
(6-5)
则

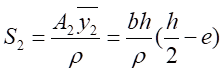
并且,令
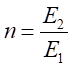
将 和
和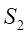 带入式(5)得:
带入式(5)得:
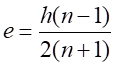 (6-6)
(6-6)
3. 推导弯曲正应力计算公式
将式(2)代入式(4),得:
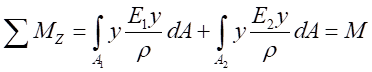
令
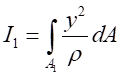 ,
,
其中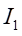 、
、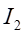 分别为截面
分别为截面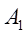 、
、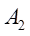 对中性轴的惯性矩。由于各梁曲率相同,经变化得:
对中性轴的惯性矩。由于各梁曲率相同,经变化得:
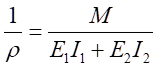 (6-7)
(6-7)
再将式(7)代入式(2),得:
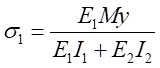 ,
,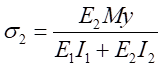 (6-8)
(6-8)
式中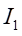 、
、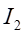 分别为
分别为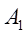 、
、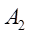 对共同中性轴Z的惯性矩。
对共同中性轴Z的惯性矩。
由单向应力状态的虎克定律公式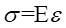 ,可求出应力实验值。应力实验值与应力理论值进行比较,以验证复合梁的正应力计算公式。
,可求出应力实验值。应力实验值与应力理论值进行比较,以验证复合梁的正应力计算公式。
2. 实验步骤
1. 首先确定单梁的物理参数,得到h=20mm,b=20mm,c=150mm。
2. 启动实验装置,将各应变片分别接到各个AB通道之间,同时把公共补偿片接到 上,并且把C通道与短接片短接。
上,并且把C通道与短接片短接。
3. 进行实验:
a.取初载荷0.5kN,每次逐级加1.0kN,直至4.5kN,总共分4次加载。
b.接完线路以及加初载荷之前都要重复置零。
c.每次加载完毕都要记录下数据。
四、实验数据
表6-1 Ⅰ梁应变数据表
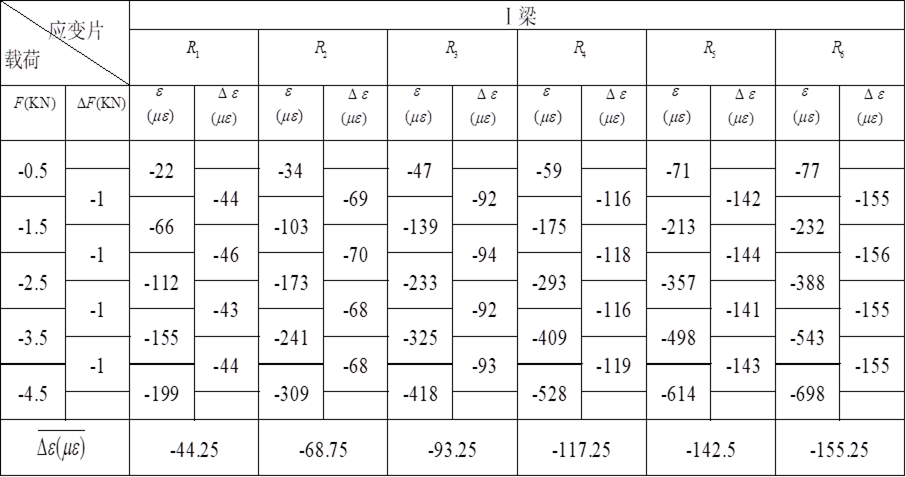
表6-2 Ⅱ梁应变数据表
 五、数据处理
五、数据处理
1. 根据实验数据计算各点的平均应变,求出各点的实验应力值,并计算出各点的理论应力值;计算实验应力值与理论应力值的相对误差。
答:根据上面实验数据,结合材料力学相关知识计算如下:
(1)由实验数据可知,各应变片处的平均应变值为:
Ⅰ梁上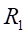 处的平均应变为:
处的平均应变为:
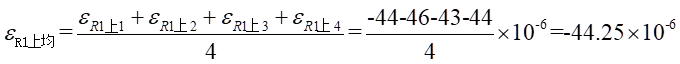
Ⅰ梁上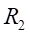 处的平均应变为:
处的平均应变为:
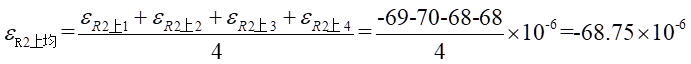
Ⅰ梁上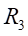 处的平均应变为:
处的平均应变为:
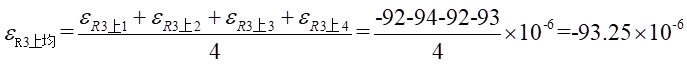
Ⅰ梁上 处的平均应变为:
处的平均应变为:
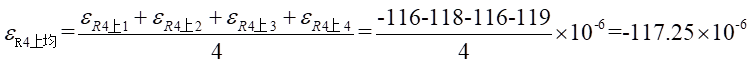
Ⅰ梁上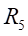 处的平均应变为:
处的平均应变为:

Ⅰ梁上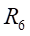 处的平均应变为:
处的平均应变为:
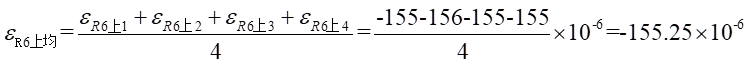
Ⅱ梁上处的平均应变为:
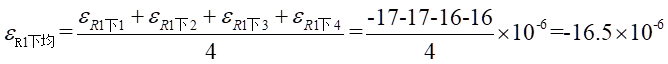
Ⅱ梁上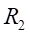 处的平均应变为:
处的平均应变为:

Ⅱ梁上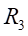 处的平均应变为:
处的平均应变为:

Ⅱ梁上 处的平均应变为:
处的平均应变为:
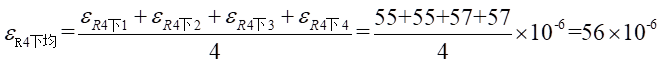
Ⅱ梁上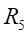 处的平均应变为:
处的平均应变为:
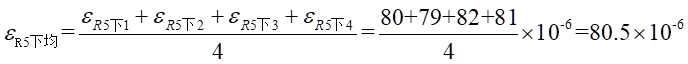
Ⅱ梁上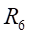 处的平均应变为:
处的平均应变为:
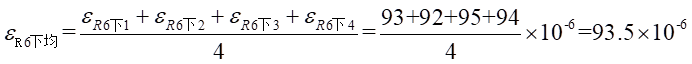
(2)各应变片处的实验应力值为:
Ⅰ梁上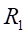 处的应力值为:
处的应力值为:
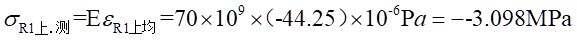
Ⅰ梁上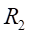 处的应力值为:
处的应力值为:
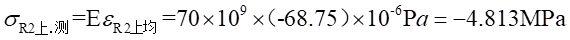
Ⅰ梁上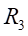 处的应力值为:
处的应力值为:
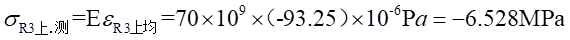
Ⅰ梁上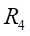 处的应力值为:
处的应力值为:
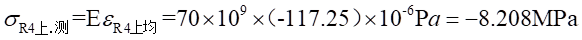
Ⅰ梁上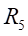 处的应力值为:
处的应力值为:
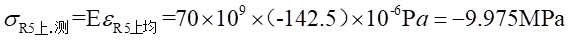
Ⅰ梁上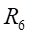 处的应力值为:
处的应力值为:

Ⅱ梁上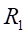 处的应力值为:
处的应力值为:
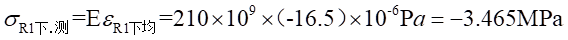
Ⅱ梁上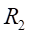 处的应力值为:
处的应力值为:
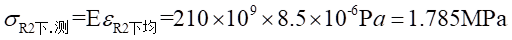
Ⅱ梁上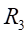 处的应力值为:
处的应力值为:
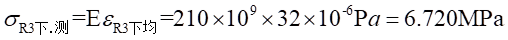
Ⅱ梁上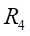 处的应力值为:
处的应力值为:
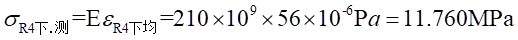
Ⅱ梁上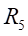 处的应力值为:
处的应力值为:
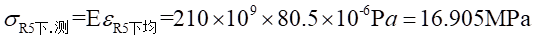
Ⅱ梁上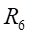 处的应力值为:
处的应力值为:
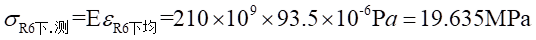
(3)理论计算试件上个应变片处的理论应力值
加载的力的大小为F=1000N。复合梁的单梁截面厚度b=20mm,高度h=20mm,截面作用点到梁支点的距离为c=150mm。设n=E2/E1=210/70=3,中性轴位置的偏移量为:
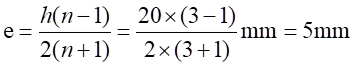
因此,可得到复合梁Ⅰ和复合梁Ⅱ正应力计算公式分别为


其中
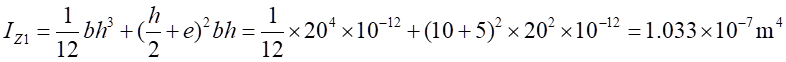

根据材料力学知识分析如下:
Ⅰ梁上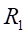 处计算应力值为:
处计算应力值为:
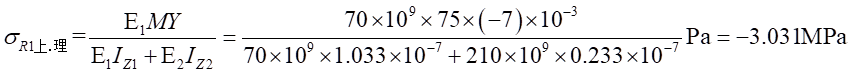
Ⅰ梁上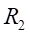 处计算应力值为:
处计算应力值为:
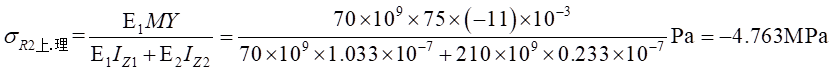
Ⅰ梁上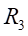 处计算应力值为:
处计算应力值为:
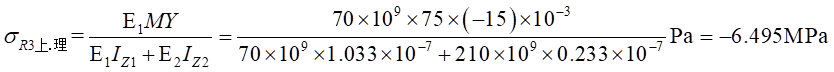
Ⅰ梁上 处计算应力值为:
处计算应力值为:
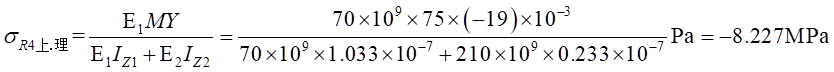
Ⅰ梁上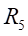 处计算应力值为:
处计算应力值为:
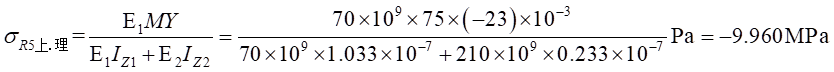
Ⅰ梁上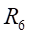 处计算应力值为:
处计算应力值为:
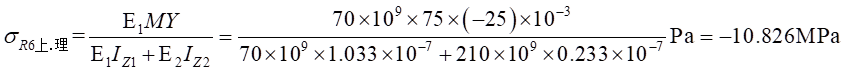
Ⅱ梁上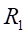 处计算应力值为:
处计算应力值为:
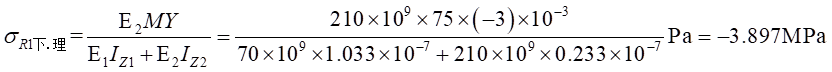
Ⅱ梁上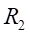 处计算应力值为:
处计算应力值为:
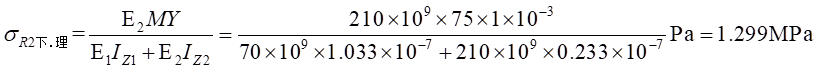
Ⅱ梁上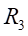 处计算应力值为:
处计算应力值为:

Ⅱ梁上 处计算应力值为:
处计算应力值为:
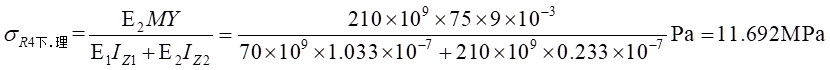
Ⅱ梁上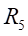 处计算应力值为:
处计算应力值为:
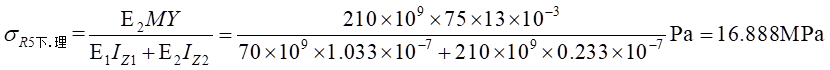
Ⅱ梁上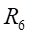 处计算应力值为:
处计算应力值为:
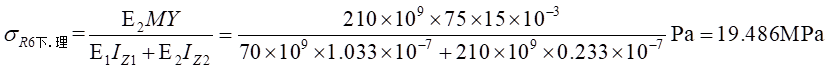
(4)计算实验应力值与理论应力值的相对误差
Ⅰ梁上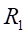 处应力值的相对误差为:
处应力值的相对误差为:

Ⅰ梁上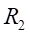 处应力值的相对误差为:
处应力值的相对误差为:
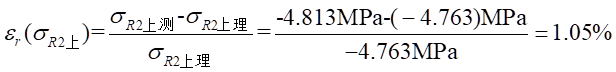
Ⅰ梁上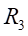 处应力值的相对误差为:
处应力值的相对误差为:

Ⅰ梁上 处应力值的相对误差为:
处应力值的相对误差为:
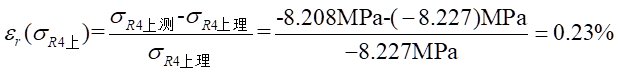
Ⅰ梁上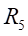 处应力值的相对误差为:
处应力值的相对误差为:

Ⅰ梁上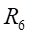 处应力值的相对误差为:
处应力值的相对误差为:
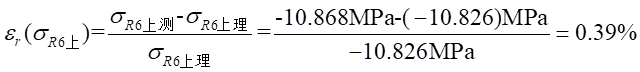
Ⅱ梁上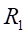 处应力值的相对误差为:
处应力值的相对误差为:

Ⅱ梁上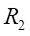 处应力值的相对误差为:
处应力值的相对误差为:

Ⅱ梁上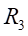 处应力值的相对误差为:
处应力值的相对误差为:
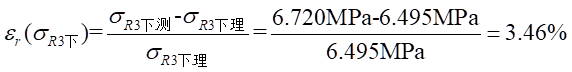
Ⅱ梁上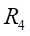 处应力值的相对误差为:
处应力值的相对误差为:
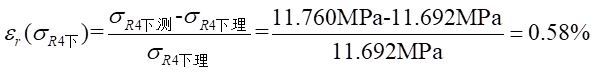
Ⅱ梁上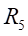 处应力值的相对误差为:
处应力值的相对误差为:
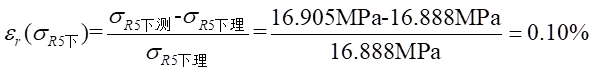
Ⅱ梁上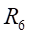 处应力值的相对误差为:
处应力值的相对误差为:
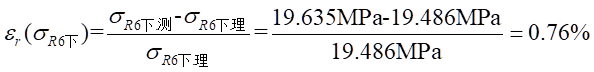
2. 上述的各点应力的实验值与应力的理论值,将两者进行比较。可以得出:实验值与理论值的结果十分接近,说明复合梁的正应力计算公式成立。
六、实验结果
根据前面计算可以看出,实验计算的结果和理论计算的结果基本吻合。现列表如下:
表6-2 结果对比表
一、实验目的
1. 用电测法测定叠梁,复合梁在弯曲受力状态下,沿其横截面高度的正应变(正应力)分布规律。
2. 推导叠梁,复合梁的正应力计算公式。
二、实验仪器和设备
1. 纯弯曲梁实验装置(纯弯曲梁复合梁)。
2. 静态数字电阻应变仪。
三、实验原理及步骤
1. 实验原理
复合梁的材料为铝梁和钢梁,上层是铝梁,其弹性模量分别为E=70GN/m2和E=210GN/m2。复合梁上总过贴上了12各应变片,每个梁各6个。
1. 几何、物理和静力学关系
以材料尺寸相同的两层矩形截面复合梁在纯弯 曲情况下为计算模型,在其纵向对称面内,承受弯矩 M的作用。上梁的弹性模量为E1,横截面面积为A1,下梁的弹性模量为E2,横截面面积为A2,且A1=A2,单梁的梁宽和梁高分别为b和h,在其纵向对称面内,承受弯矩M的作用。两种不同的材料由胶粘合制成。下面建立横截面上的弯曲正应力公式,平面假设与单向假设均成立。
设中性层的曲率半径为
(1)变形几何关系。根据平面假设可知,横截面上y处的纵向正应变为:
(2)物理关系。依胡克定律
(3)静力学平衡关系。根据受力分析,由静力学平衡关系,考虑横截面上内力的平衡,
由
2. 确定中性层位置
将式(2)代入式(3)中,得
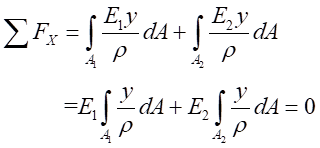
令
则
则
并且,令
将
3. 推导弯曲正应力计算公式
将式(2)代入式(4),得:
令
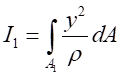 ,
,
其中
再将式(7)代入式(2),得:
式中
由单向应力状态的虎克定律公式
2. 实验步骤
1. 首先确定单梁的物理参数,得到h=20mm,b=20mm,c=150mm。
2. 启动实验装置,将各应变片分别接到各个AB通道之间,同时把公共补偿片接到
3. 进行实验:
a.取初载荷0.5kN,每次逐级加1.0kN,直至4.5kN,总共分4次加载。
b.接完线路以及加初载荷之前都要重复置零。
c.每次加载完毕都要记录下数据。
四、实验数据
表6-1 Ⅰ梁应变数据表
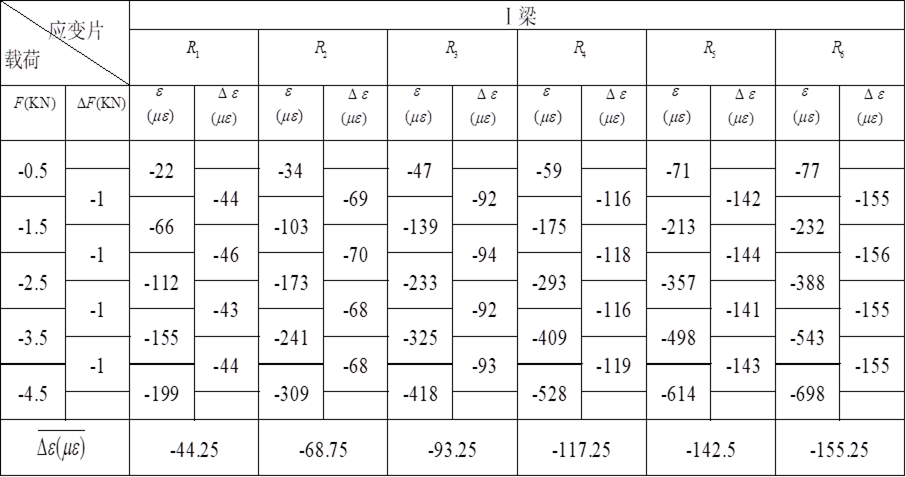
表6-2 Ⅱ梁应变数据表
 五、数据处理
五、数据处理1. 根据实验数据计算各点的平均应变,求出各点的实验应力值,并计算出各点的理论应力值;计算实验应力值与理论应力值的相对误差。
答:根据上面实验数据,结合材料力学相关知识计算如下:
(1)由实验数据可知,各应变片处的平均应变值为:
Ⅰ梁上
Ⅰ梁上
Ⅰ梁上
Ⅰ梁上
Ⅰ梁上
Ⅰ梁上
Ⅱ梁上处的平均应变为:
Ⅱ梁上
Ⅱ梁上
Ⅱ梁上
Ⅱ梁上
Ⅱ梁上
(2)各应变片处的实验应力值为:
Ⅰ梁上
Ⅰ梁上
Ⅰ梁上
Ⅰ梁上
Ⅰ梁上
Ⅰ梁上
Ⅱ梁上
Ⅱ梁上
Ⅱ梁上
Ⅱ梁上
Ⅱ梁上
Ⅱ梁上
(3)理论计算试件上个应变片处的理论应力值
加载的力的大小为F=1000N。复合梁的单梁截面厚度b=20mm,高度h=20mm,截面作用点到梁支点的距离为c=150mm。设n=E2/E1=210/70=3,中性轴位置的偏移量为:
因此,可得到复合梁Ⅰ和复合梁Ⅱ正应力计算公式分别为
其中
根据材料力学知识分析如下:
Ⅰ梁上
Ⅰ梁上
Ⅰ梁上
Ⅰ梁上
Ⅰ梁上
Ⅰ梁上
Ⅱ梁上
Ⅱ梁上
Ⅱ梁上
Ⅱ梁上
Ⅱ梁上
Ⅱ梁上
(4)计算实验应力值与理论应力值的相对误差
Ⅰ梁上
Ⅰ梁上
Ⅰ梁上
Ⅰ梁上
Ⅰ梁上
Ⅰ梁上
Ⅱ梁上
Ⅱ梁上
Ⅱ梁上
Ⅱ梁上
Ⅱ梁上
Ⅱ梁上
2. 上述的各点应力的实验值与应力的理论值,将两者进行比较。可以得出:实验值与理论值的结果十分接近,说明复合梁的正应力计算公式成立。
六、实验结果
根据前面计算可以看出,实验计算的结果和理论计算的结果基本吻合。现列表如下:
表6-2 结果对比表
| 梁 | Ⅰ梁 | Ⅱ梁 | ||||||||||
| 应变片 |
|
|
|
|
|
|
|
|
|
|
|
|
| 相对中性轴的坐标y/mm | -7 | -11 | -15 | -19 | -23 | -25 | -3 | 1 | 5 | 9 | 13 | 15 |
| 实验应力值/MPa | -3.1 | -4.8 | -6.5 | -8.2 | -10.0 | -10.9 | -3.5 | 1.8 | 6.7 | 11.8 | 16.9 | 19.6 |
| 理论应力值/MPa | -3.0 | -4.8 | -6.5 | -8.2 | -10.0 | -10.8 | -3.9 | 1.3 | 6.5 | 11.7 | 16.9 | 19.5 |
| 相对误差/% | 2.2 | 1.1 | 0.5 | 0.2 | 0.2 | 0.4 | 11.1 | 37.4 | 3.5 | 0.6 | 0.1 | 0.8 |
从表中可以看出,理论计算和实验结果基本吻合,相对误差不大。实验从某种方面上证实了理论知识。数据可用。
七、思考题
1. 复合梁中性层为何偏移?
答:因为两种材料的抗弯能力以及抗拉能力不同,导致在同等应力条件下,两个截面对称位置发生的应变不同。抗弯能力以及抗拉能力强的材料发生的变形小于另一种材料,因此中性层就向下偏移了。
2. 如何理解复合梁实验中出现两个中性层?
复合梁虽然中间是由物理或化学方法进行了连接,但是其实际上不是一个材料性质连续的整体。因此在两种材料的交界面上会产生应力的突变,在整个复合梁的横截面上,应力不是连续的,因此可能出现两个中性层。
七、思考题
1. 复合梁中性层为何偏移?
答:因为两种材料的抗弯能力以及抗拉能力不同,导致在同等应力条件下,两个截面对称位置发生的应变不同。抗弯能力以及抗拉能力强的材料发生的变形小于另一种材料,因此中性层就向下偏移了。
2. 如何理解复合梁实验中出现两个中性层?
复合梁虽然中间是由物理或化学方法进行了连接,但是其实际上不是一个材料性质连续的整体。因此在两种材料的交界面上会产生应力的突变,在整个复合梁的横截面上,应力不是连续的,因此可能出现两个中性层。


